|
|
ГЛАВА 3. МЕХАНИЗМЫ ДВИЖЕНИЯ ДОМЕННЫХ И МЕЖФАЗНЫХ
ГРАНИЦ В СЕГНЕТОЭЛЕКТРИКАХ. АНАЛИТИЧЕСКОЕ РАССМОТРЕНИЕ
Для построения более общей, чем у
предшественников аналитической модели поляризации и переполяризации СЭ на НЧ и
ИНЧ , связанной с различными механизмами движения ДГ и МГ (релаксационным и
гистерезисным), было рассмотрено движение ДГ и МГ, вызванное зарождением
ступенчатых доменов, активированных электрическим полем (в отличие от
рассмотренного Миллером, Вайнрайхом [1] термически активированного процесса
зародышеобразования) на уже существующих ДГ и МГ . В результате рассмотрения
получено уравнение движения ДГ и МГ в следующем виде :
![]() , (1)
, (1)
где
х и ![]() - смещение и скорость
ДГ , h и F
- эффективные коэффициенты
вязкого и сухого трения , k -
эффективный коэффициент квазиупругой силы, Ps - спонтанная
поляризация, Е - напряженность электрического поля.
- смещение и скорость
ДГ , h и F
- эффективные коэффициенты
вязкого и сухого трения , k -
эффективный коэффициент квазиупругой силы, Ps - спонтанная
поляризация, Е - напряженность электрического поля.
Заметим,
что (1) представляет собой более общий случай уравнения, предложенного
Шильниковым [2], а также Поповым и Шуваловым [3], для СЭ, ранее использованного
Кителем и Галтом [4] для ферромагнетиков . В нашем случае, в уравнении (1)
впервые учтен в аналитическом виде член, отражающий силу типа силы сухого
трения, действующую на ДГ и МГ в процессе их движения. С помощью компьютерного
моделирования уравнения (1) получена ПП следующего вида (Рис. 1).
|
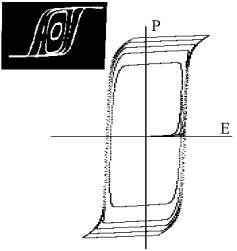
Рис. 1.
Смоделированная петля поляризации по уравнению (1). На вставке приведен вид
петель поляризации кристалла ТГС в полях Е0=1, 2 В/см n=50Гц при
Т=22.5°С [2]. |
|
|
Естественно, что в общем случае на
зародышеобразование сильное влияние оказывают термические флуктуации
(термическая активация). В частности, в результате влияния последних ДГ и МГ
могут двигаться под действием электрического поля с напряженностью, меньшей
значения напряженности порогового поля, определяемого только силой сухого
трения. Для учета этого явления в уравнение (1) была введена сила ![]()
![]() , которая является
промежуточной силой между силами сухого и вязкого трения. При b=1
эффективная сила трения по преимуществу является силой вязкого трения, а при b =
0 она в основном моделирует силу сухого трения. Тогда уравнение (1) можно
переписать в виде
, которая является
промежуточной силой между силами сухого и вязкого трения. При b=1
эффективная сила трения по преимуществу является силой вязкого трения, а при b =
0 она в основном моделирует силу сухого трения. Тогда уравнение (1) можно
переписать в виде
![]() , (2)
, (2)
заметив,
что в обоих случаях [ и (1), и (2)] на ДГ и (или) МГ действует , кроме того , и
квазиупругая возвращающая сила вида kx.
На
рис. 2 показан пример ПП , получаемых в этом случае при b=0.5
.
Для ПП, получаемых из уравнения (2)
при b=0.5 для различных значений напряженности электрического
поля E, после их обработки
на ЭВМ, были кроме того получены полевые зависимости действительной e'
(E) и мнимой e"
(E) составляющих
комплексной эффективной диэлектрической проницаемости . При этом сравнение полученных полевых зависимостей e*(E) с подобными же эмпирическими зависимостями
[2] показало их хорошее согласие.
|
Рис. 3. Смоделированные
петли поляризации по уравнению (3) при b=0.05, n=5. На вставке приведен вид петель
поляризации кристалла ТГС в полях Е0=50, 100, 200, 500 В/см n=50 Гц при
Т=22.5°С [2]. |
При действии достаточно сильных (близких к насыщающим)
электрических полей в сегнетоэлектрических образцах происходят процессы
монодоменизации, сопровождающиеся резким уменьшением количества ДГ при росте
напряженности поля. При этом квазиупругую силу уже нельзя считать линейной, в
связи с чем возникает необходимость введения нелинейных членов квазиупругой
силы. В силу симметрийной эквивалентности среднего смещения ДГ в положительном
и отрицательном направлениях ненулевыми нелинейными членами квазиупругой силы
являются только члены с нечетными степенями по х. При этом уравнение движения
ДГ приобретает вид :
![]() , (3)
, (3)
а смоделированные
ПП имеют форму, изображенную на рис. 3.
|
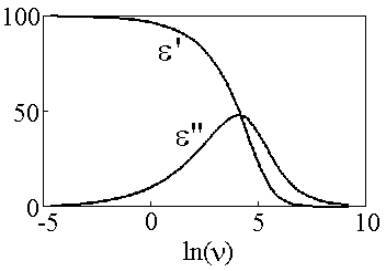
Рис. 4. Частотные
зависимости действительной e'(n) и мнимой e"(n)
составляющих комплексной эффективной диэлектрической проницаемости для петель
поляризации, полученных из уравнения (2) при b=0.5. |
Следует отметить, что внутренние поля, создаваемые дефектами недоменной
природы, могут приводить к неэквивалентности среднего смещения ДГ в
положительном и отрицательном направлениях.
В этом случае в уравнении движения ДГ могут
появиться члены с четными степенями по х , а ПП будет характеризоваться
униполярностью.
По аналогии с амплитудными зависимостями из уравнения (2) при b=0.5
были получены частотные зависимости e'(n) и e"(n).
На рис. 4 представлены кривые таких зависимостей, полученные из обсчета
смоделированных ПП. Хорошо видно, что частотные зависимости e'(n)
и e"(n)
имеют вид, подобный классическим дисперсионным кривым e* . Однако, эти кривые не описываются
уравнениями Дебая и (или) Коула-Коула.
Одновременно подчеркнем, что
рассматриваемая модель применима как для синусоидальных, так и несинусоидальных
(П-импульсных ) полей. В последнем случае, модель позволяет анализировать
особенности взаимодействия и механизмы срыва ДГ с точечных дефектов по
временной зависимости тока переключения при воздействии П-импульсного
электрического поля.
В рамках предложенной модели
произведена оценка соотношения вкладов релаксационного и гистерезисного
механизмов движения ДГ при процессах старения в сегнетоэлектрике NaNO2 . Так, например, вычисление величины b в уравнении
(2) для данного случая даёт значение b=1/3. На основании этого сделан вывод о
существенном влияния "сильных" дефектов на самопроизвольное движение
ДГ при процессах старения в NaNO2 .
Таким образом, получена достаточно
универсальная модель, позволяющая проводить анализ экспериментальных ПП с
помощью ЭВМ и (на основе этого анализа) судить о механизмах движения ДГ и МГ и
характере сил, действующих на них в процессе поляризации и переполяризации
сегнетоэлектриков, а также в процессе их старения.
|
|
|||
|
|
Copyright © 2001 Нестеров
Владимир Николаевич nv2-nesterov@narod.ru |
||
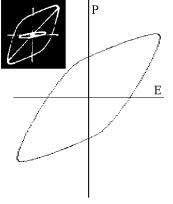
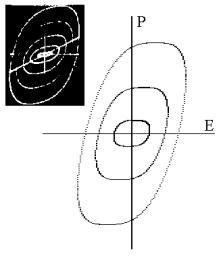 Рис. 2. Смоделированные петли поляризации по уравнению (2)
при
Рис. 2. Смоделированные петли поляризации по уравнению (2)
при